Resumen
Palabras ClavesEn este trabajo se abordan las estructuras fractales y algoritmos para producirlas mediante el uso de funciones recursivas. Principalmente se explica como realizar fractales mediante la replicación recursiva de patrones, primero rectangulares y luego por segmentos.
Fractales, Funciones Recursivas, Curvas de Koch
Las estructuras fractales
Una estructura fractal es un objeto que repite sus formas geométricas a diferentes escalas, es decir que guarda semejanza consigo mismo. La geometría fractal escapa a la geometría euclidiana y ha resultado mucho más útil que esta para poder describir ciertos patrones de la naturaleza. Es más sencillo describir la forma de una hoja de árbol con una estructura fractal que hacerlo con los elementos euclidianos (el círculo, el cuadrado, etc. etc.). En la figura debajo se puede ver un fractal que reproduce la forma de una planta.
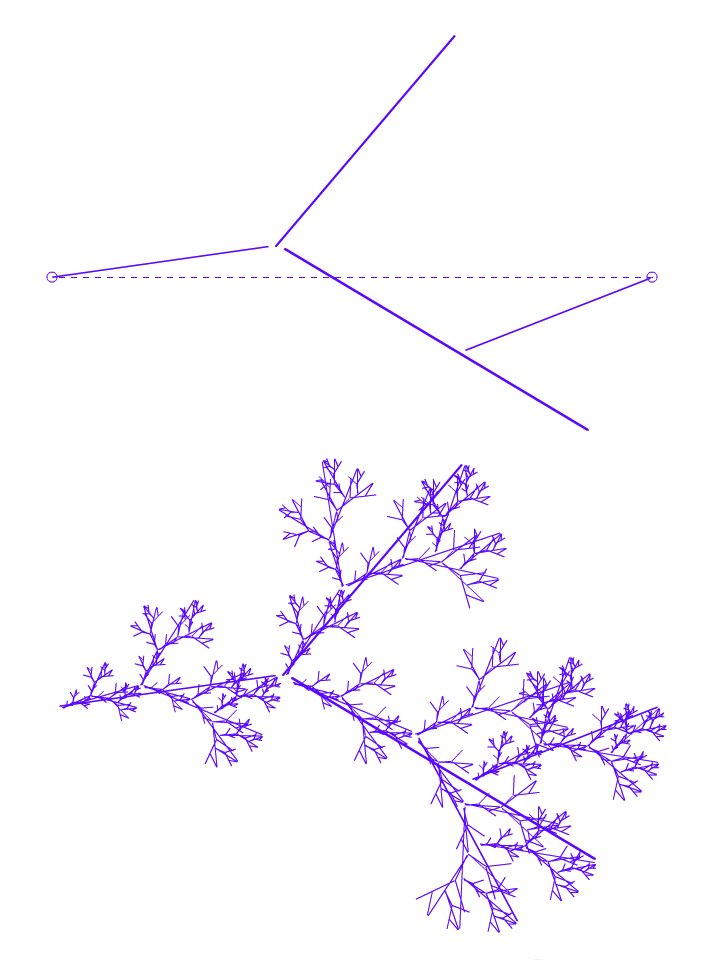
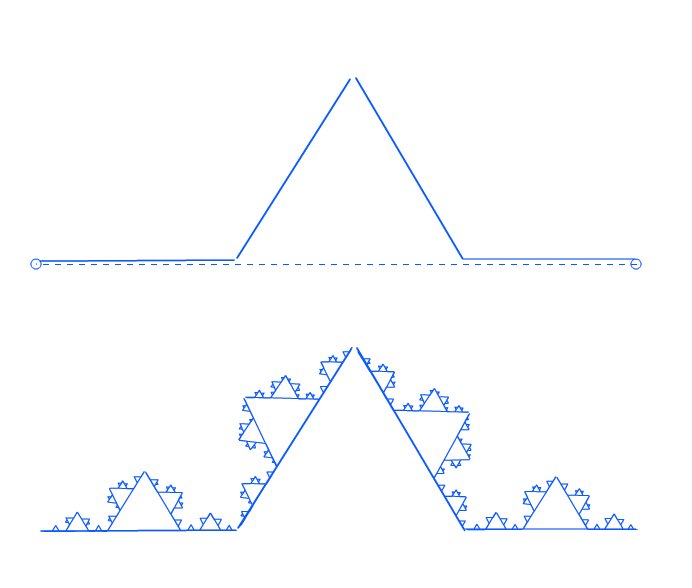
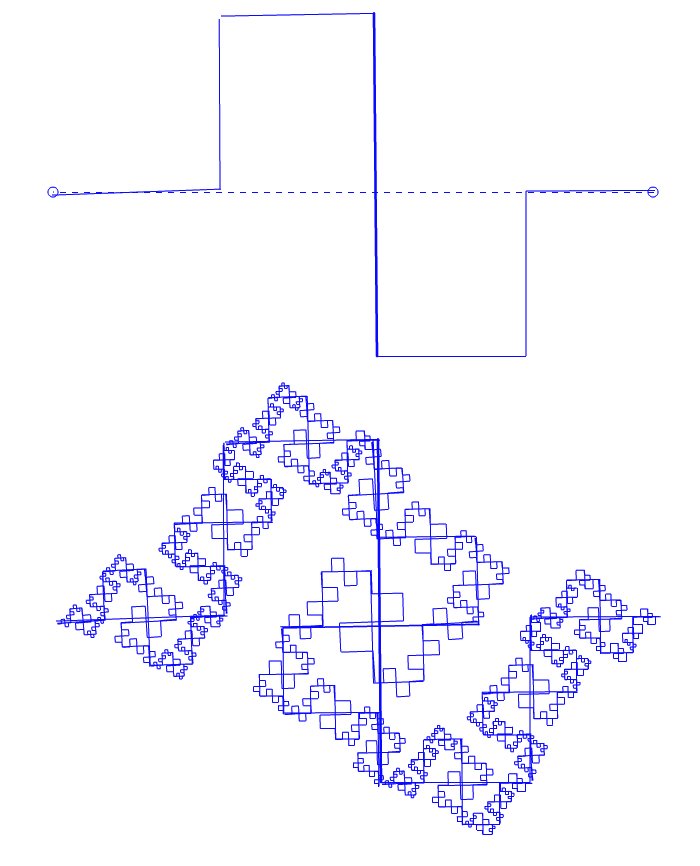
En las imágenes de arriba se pueden ver dos figuras, la de arriba cumple dos funciones: por un lado es la base sobre la que se va a replicar la semilla, y por otro es la semilla misma a ser replicada. ¿Qué significa replicar en este caso? La idea es, por cada segmento en la figura base, se repite la semilla completa, respetando su ubicación, tamaño y orientación. Este procedimiento se lleva a cabo, luego, sobre los segmentos resultantes y luego sobre los nuevos, y así hasta el infinito. Por supuesto, en la computadora no hay infinito y por lo tanto es necesario establecer la condición de corte del procedimiento: hacerlo n-veces ó hacerlo hasta que los dibujos tengan un tamaño ya no visible (menor al pixel). Estos casos que expongo son una casos particular que se desprenden de las Curvas de Koch, un tipo muy conocido de figuras fractales. En las Curvas de Koch, a diferencia de nuestro ejemplo, los segmentos originales son quitados y reemplazados por las nuevas figuras (réplicas), y en general parten de polígonos regulares. En la siguiente figura podemos ver una caso que asemeja una conocida Curva de Koch.
En esta, es más sencillo ver cómo en cada uno de estos 4 segmentos se replica el mismo motivo y así sucesivamente. No es mi intensión explayarme sobre la teoría general de los fractales en este texto, sino desarrollar la producción técnica de alguno de estos.
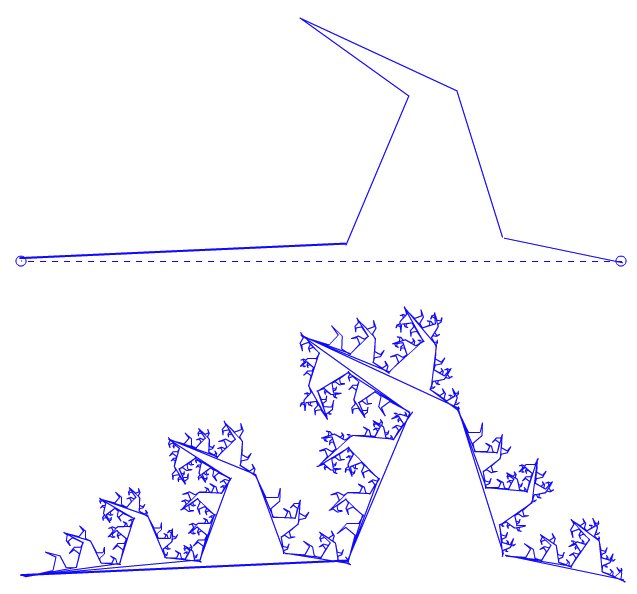
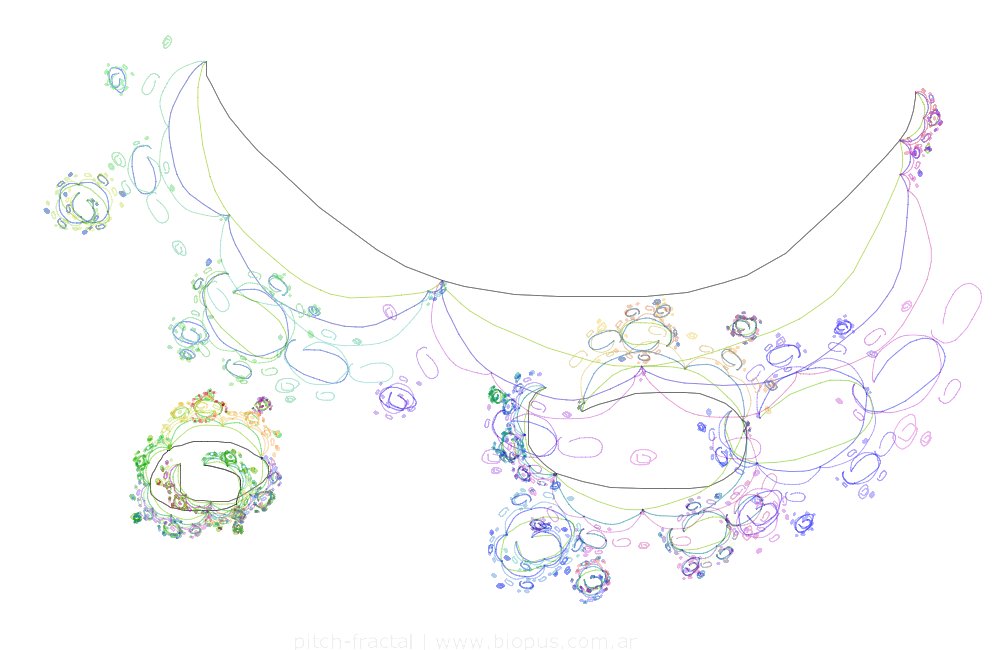
El ejemplo de abajo muestra otro patrón conocido. Los ejemplos aquí mostrados están desarrollado con una aplicación que realice hace unos años y que me permite dibujar la semilla que se replicará sobre sí misma. Esta posibilidad de trazar los segmentos manualmente hace que las relaciones geométricas de estos ejemplos no sean perfectas, lo que desde mi perspectiva agrega interés al resultado, ya que combina esa relación entre orden y desorden de la que habla Galanter en sus textos.
En la siguiente figura, aprovecho más aún la posibilidad de hacer figuras irregulares y, a partir de eso, obtener resultados de gran riqueza.
En las siguientes figuras exploto la posibilidad de realizar trazos inconexos y con mayor nivel de irregularidad:
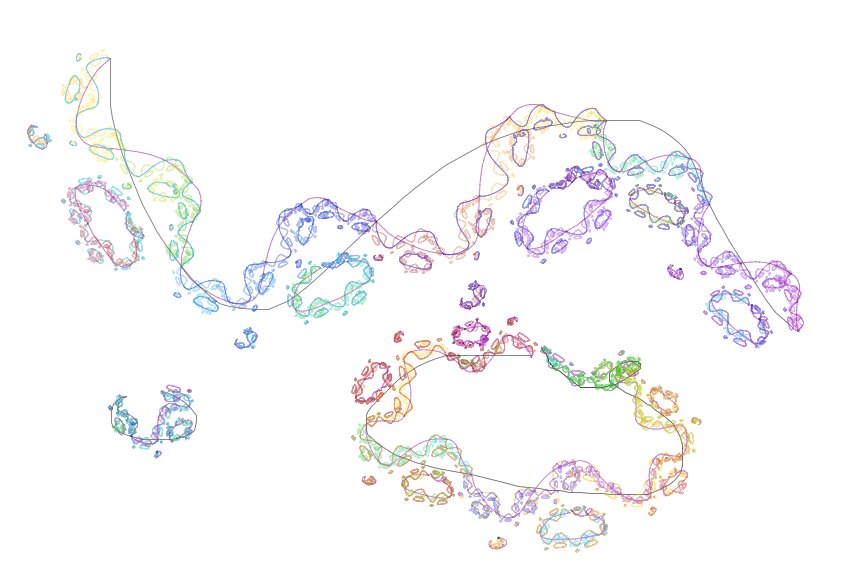
Posterior a la aplicación citada, desarrollé una en la que la semilla es son trazos a mano alzada (hechas con el mouse), estos trazos (en apariencia curvos) se descomponen en pequeñísimos segmentos rectos, lo que permite utilizar básicamente el mismo procedimiento. En realidad, cabe hacer una aclaración, en este tipo de trazos no es conveniente hacer la réplica "uno por uno", ya que los segmentos son demasiado pequeños y la disminución de escala en cada sucesivo nivel de réplica hace imposible producir un resultado perceptible. Por eso, en estos ejemplos, la estrategia es transgredida, tomando porciones de curvas (es decir varios segmentos) como un único segmento a la hora de replicar. Lo importante es que se sigue conservando el criterio de autosimilitud a diferentes escalas. Podemos ver un ejemplos realizado con dicha aplicación, realizada para una instalación llamada "Gesto Fractal" (en el colectivo Proyecto Biopus).
Obviamente, la aparición de los trazos curvos han aumentado la plasticidad en la estética de las figuras.
Fractales con Rectángulos
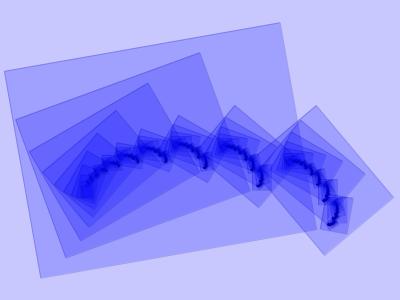
Todos los ejemplos mostrados aquí se basan en la utilización de funciones recursivas como estrategia constructiva. Debajo pueden verse dos imágenes fractales construidas con rectágulos que replican a diferentes escalas su relación con el marco, tomando cada nuevo rectángulo como un nuevo marco de los que están en su interior. La semilla son sólo dos rectángulos levemente superpuestos, pero que en la sucesiva replicación generan patrones complejos. La imagen de arriba es la semilla y debajo la fractalización:
Ejemplo Fractal 01
A continuación podemos ver el código fuente que genera dicho fractal. El programa está desarrollado en Processing .
int cantidad = 2; float factor[] = { 0.7 , 0.3 }; float x[] = { 0.4 , 0.8 }; float y[] = { 0.5 , 0.6 }; float ang[] = { radians(-10) , radians(50) }; //--------------------------------------- void setup() { size( 400, 300 ); smooth(); stroke( 0 , 0 , 155 , 50 ); fill( 0 , 0 , 255 , 50 ); } //--------------------------------------- void draw() { background(200,200,255); fractal( 10, 400, 300 ); noLoop(); } //--------------------------------------- void fractal( int nivel, float ancho, float alto ) { if ( nivel>0 ) { rectMode( CENTER ); for ( int i=0 ; i<cantidad ; i++ ) { pushMatrix(); translate( ancho*x[i], alto*y[i] ); rotate( ang[i] ); rect( 0, 0, ancho*factor[i], alto*factor[i] ); translate( ancho*factor[i]*-0.5, alto*factor[i]*-0.5 ); fractal( nivel-1, ancho*factor[i], alto*factor[i] ); popMatrix(); } } }Hecho en Processing
El algoritmo mostrado arriba se encarga de tomar información respecto de los rectángulos que conforman la semilla, para luego replicar dicho patrón en el interior de estos y así con cada nuevo rectángulo resultante de dicha réplica. La información de los rectángulos está contenida en cuatro arreglos llamados: x[], y[], factor[], ang[], que representa las posiciones en X e Y, el tamaño y el ángulo, respectivamente. Por ejemplo, en las siguientes líneas al inicio del código citado:
float factor[] = { 0.7 , 0.3 }; float x[] = { 0.4 , 0.8 }; float y[] = { 0.5 , 0.6 }; float ang[] = { radians(-10) , radians(50) };Hecho en Processing
se establece que el primer rectángulo tiene un tamaño del 70% respecto del marco y el segundo de un 30%, esto figura en la primer línea en donde el arreglo factor[], tiene un valor de 0.7 y 0.3 para sus valores. Todos los valores (excepto los ángulos) están normalizados, es decir que se mantienen en un rango entre 0 y 1. En el caso del factor[] (cuyo nombre responde a que es un "factor de multiplicación") sus valores son relativos a las dimensiones del marco que los contiene, es decir que un 0.7 corresponde al 70% del tamaño del marco contenedor. Lo mismo vale para x[] e y[]. Los ángulos también como eje de referencia la rotación que posee el marco que los contiene.
Es fácil notar que el algoritmo que produce el fractal es extremadamente corto en relación con la complejidad y cantidad de figuras que genera. Esto se debe a que implementa una función recursiva, esto es una función que se invoca a sí misma en su propio cuerpo. La función es cuestión se llama fractal(), y recibe como parámetros el nivel de réplica, el ancho y el alto del marco que lo contiene:
void fractal( int nivel, float ancho, float alto ) {Hecho en Processing
en su interior puede verse como se invoca a sí misma en la siguiente línea:
fractal( nivel-1, ancho*factor[i], alto*factor[i] );Hecho en Processing
y es en esta línea dónde se produce la autosimulitud, ya que esta invocación pide desarrollar nuevamente el fractal pero en el tamaño del actual factor[]. La función tiene un ciclo for que se encarga de recorrer todos los rectángulos del patrón (la semilla), y lo que hace es dibujar cada uno de los rectágulos en su posición, rotación y tamaño:
translate( ancho*x[i], alto*y[i] ); rotate( ang[i] ); rect( 0, 0, ancho*factor[i], alto*factor[i] );Hecho en Processing
para luego invocar a la misma función fractal() para replicarse en el interior del rectángulo recién dibujado. Dentro del ciclo for, está el siguiente condicional:
if ( nivel>0 ) {Hecho en Processing
el mismo se encarga de limitar las iteraciones, ya que sino el programa caería en un bucle infinito. Por eso, al invocar por primera vez la función fractal() en la estructura draw():
void draw() { background(200,200,255); fractal( 10, 400, 300 ); }Hecho en Processing
al primer parámetro, correspondiente al nivel, se le asigna un valor de 10, esto quiere decir que la estructura se replicará 10 veces hacia adentro.
Fractales con secuencias de segmentos
En el programa que trataremos a continuación los fractales se producen a partir de segmentos rectos. Estos segmentos se definen a través de las coordenadas de los puntos ubicados en sus extremos. Así cada segmento tiene coordenadas X1, Y1, X2 y Y2. Estas coordenadas están normalizadas, es decir que están en el rango 0..1 en donde 1 es la distancia entre dos puntos de referencia que funcionan como marco. En el programa que sigue el algoritmo toma los puntos (50, 300) y (370, 300) como extremos para replicar el primer patrón. A continuación podemos ver el algoritmo completo:
int profundidad = 1; int cantidad = 3; float x1[] = { 0.0, 0.3, 0.3 }; float y1[] = { 0.0, -0.1, -0.1 }; float x2[] = { 0.3, 0.5, 1.0 }; float y2[] = { -0.1, 0.5, -0.3 }; //--------------------- void setup() { size( 500, 500 ); frameRate(1); smooth(); } //--------------------- void draw() { profundidad = (profundidad+1) % 12; background( 255 ); fractal( profundidad, 50, 300, 370, 300 ); } //--------------------- void fractal( int nivel, float xp1, float yp1, float xp2, float yp2 ) { if ( nivel>0 ) { float verde = map( nivel, 0, profundidad, 0, 255 ); float azul = map( nivel, 0, profundidad, 255, 0 ); float alfa = map( nivel, 0, profundidad, 20, 250 ); stroke( verde, 0, azul, alfa ); float distancia = dist( xp1, yp1, xp2, yp2 ); float angulo = atan2( yp2-yp1, xp2-xp1 ); if ( distancia>0 ) { pushMatrix(); translate( xp1, yp1 ); rotate( angulo ); for ( int i=0 ; i<cantidad ; i++ ) { float nx1 = x1[i] * distancia; float ny1 = y1[i] * distancia; float nx2 = x2[i] * distancia; float ny2 = y2[i] * distancia; line( nx1, ny1, nx2, ny2 ); fractal( nivel-1, nx1, ny1, nx2, ny2 ); } popMatrix(); } } }Hecho en Processing
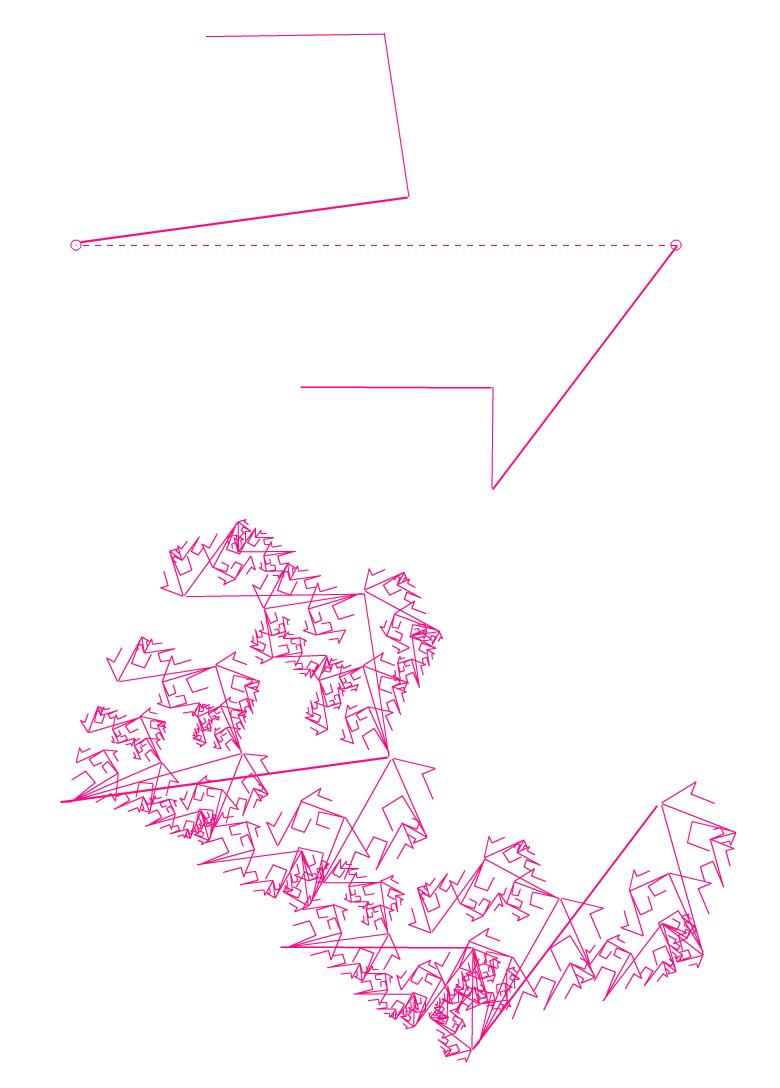
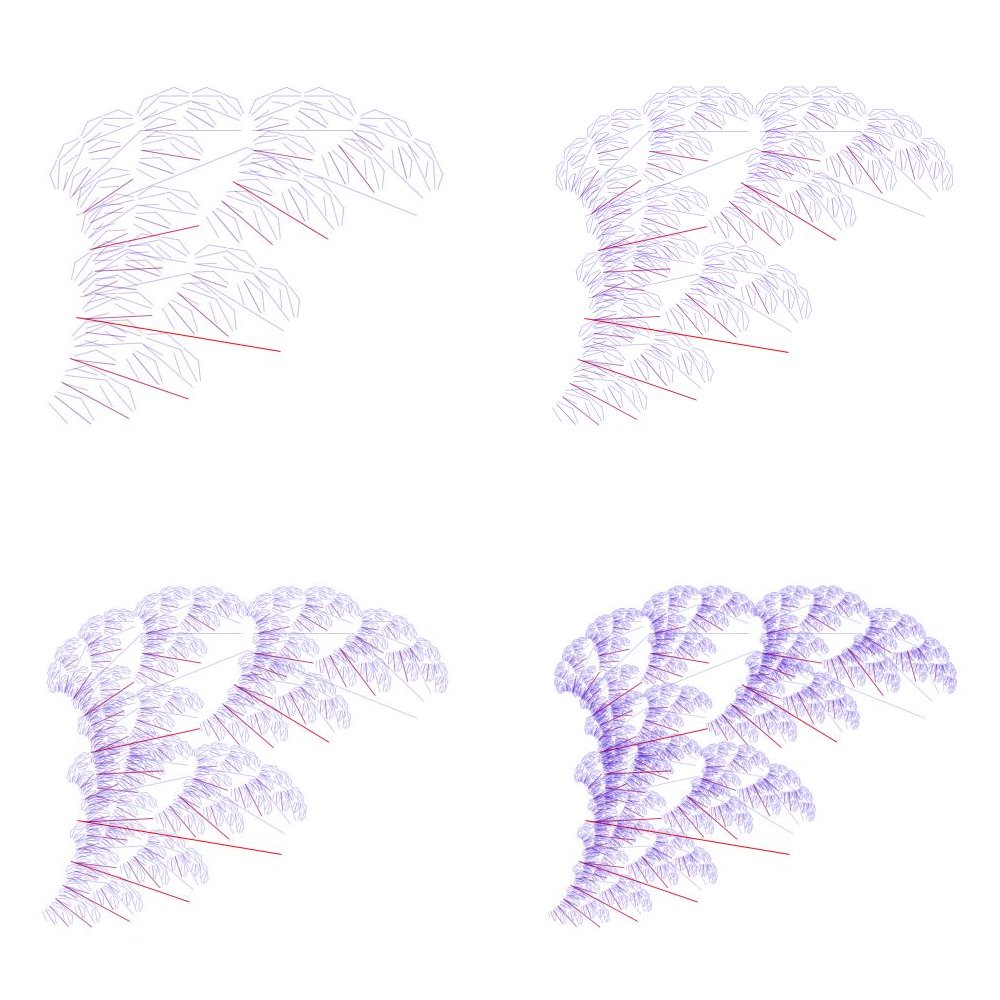
En el ejemplo, la cantidad de segmentos es 3. El algoritmo reproduce en cada segmento el patrón de los tres mismos segmentos, adaptando dicho patrón a la posición, tamaño y rotación que el segmento de base posee. Así, de los 3 segmentos originales, saldrán 9 (3 por cada uno) nuevos segmentos, que luego traerán otros 27 y así sucesivamente. En las imágenes que siguen podemos ver la secuencia de imágenes que muestran como se agrega en cada iteración un nuevo nivel, reproduciendo nuevamente los 3 segmentos del patrón en cada segmento existente (creado en la iteración anterior). A cada iteración le llamaremos también "estrato", considerando que cada una aporta una nueva capa de complejidad a la imagen.
Figuras: secuencia del proceso recursivo desde 1 hasta 4 estratos
Ejemplo Fractal 02
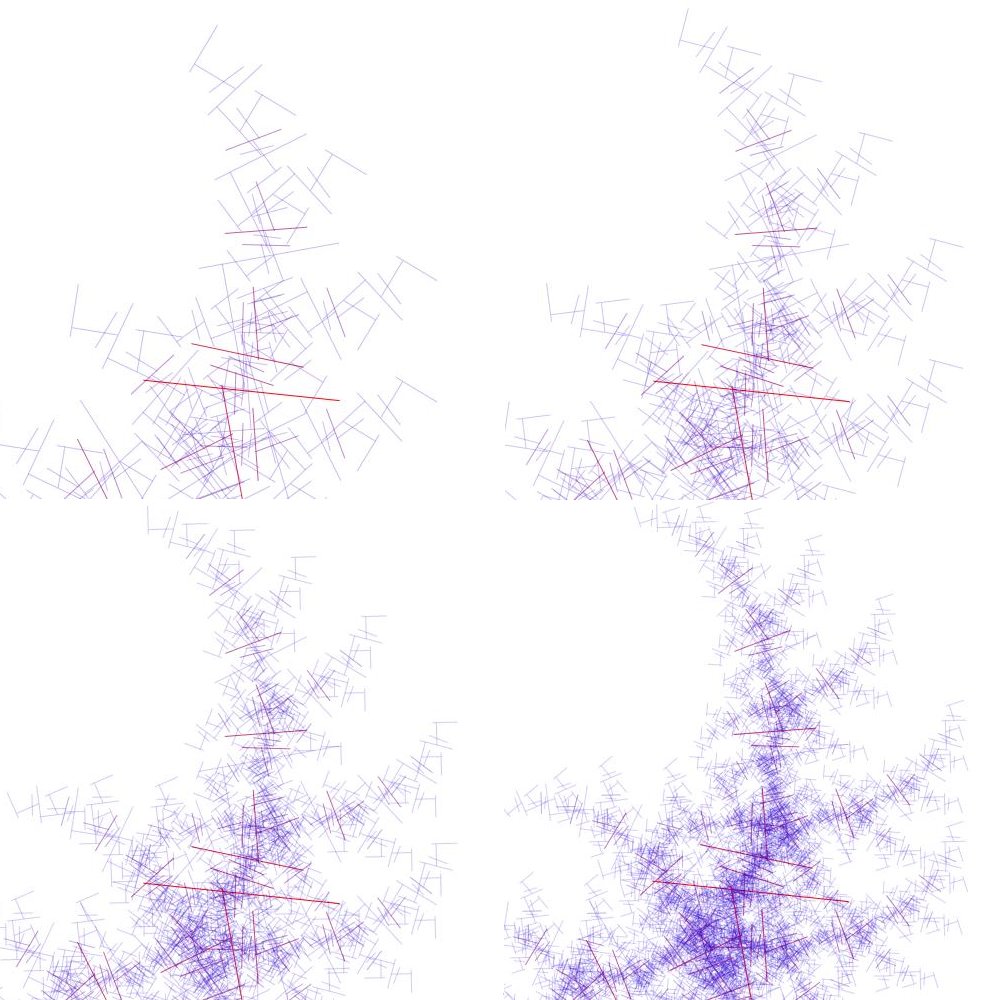
Figuras: secuencia del proceso recursivo desde 5 hasta 8 estratos
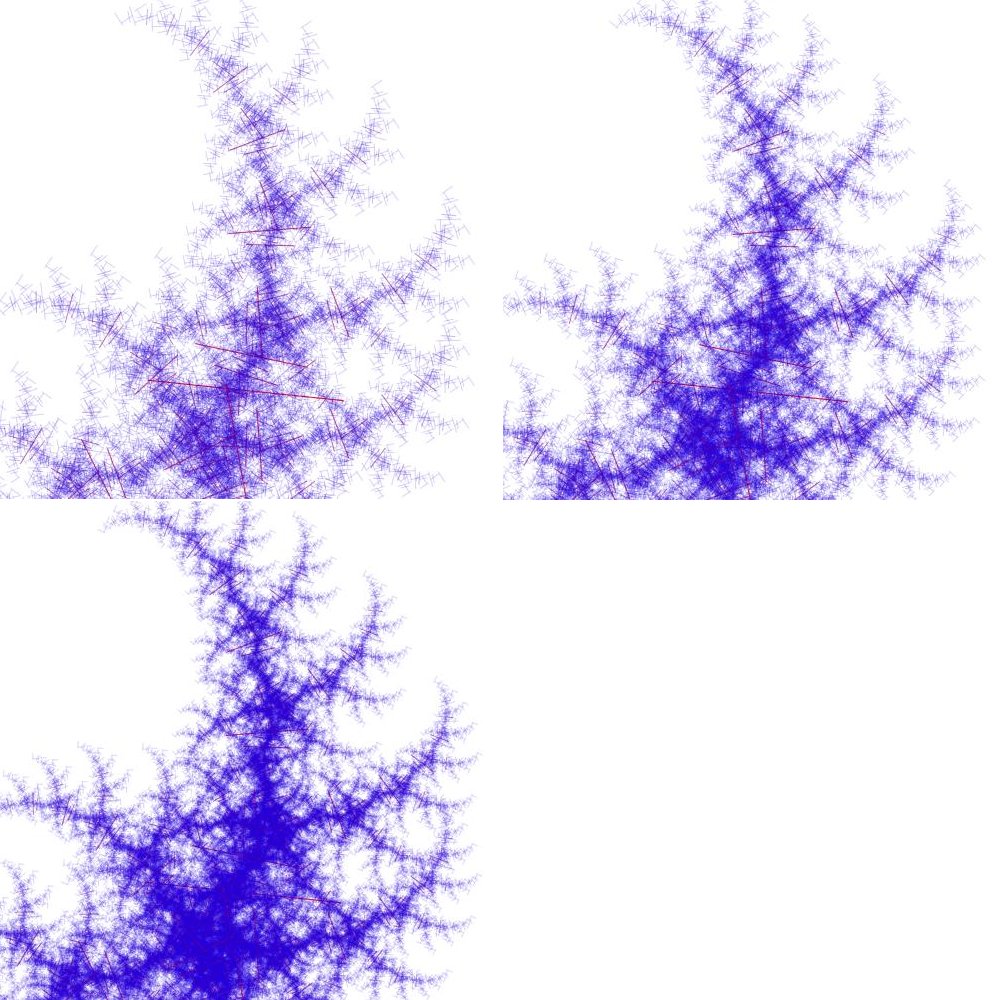
Figura: proceso recursivo con 12 estratos
Como se puede ver en esta última imagen, la complejidad y detalle que se puede alcanzar es muy alto, por supuesto a un costo computacional no menor.
La función fractal recibe como parámetros el nivel (estrato de iteración) y los 4 parámetros correspondientes a los dos extremos del segmento de base: X1, Y1, X2, Y2. La función fractal( ) recibe el nivel y las coordenadas.
void fractal( int nivel, float xp1, float yp1, float xp2, float yp2 ) {Hecho en Processing
Si el nivel no ha llegado a cero, entonces calcula la distancia y ángulo de rotación de los puntos recibidos para ubicar el patrón de segmentos.
if ( nivel>0 ) { ... float distancia = dist( xp1, yp1, xp2, yp2 ); float angulo = atan2( yp2-yp1, xp2-xp1 );Hecho en Processing
Realiza los movimientos, verificando primero que la distancia entre los puntos es mayor a cero:
if ( distancia>0 ) { ... translate( xp1, yp1 ); rotate( angulo );Hecho en Processing
Por último recorre todos los segmentos del patrón, calculando sus posiciones absolutas en función del segmento de base en el que se replican. Estas nuevas coordenadas son utilizadas para dibujar el segmento y a su vez vuelve a llamar (en forma recursiva) a la misma función fractal( ) pasando al nuevo segmento como base para volver a realizar todo el procedimiento, es decir, replicar el patrón:
for ( int i=0 ; i<cantidad ; i++ ) { float nx1 = x1[i] * distancia; float ny1 = y1[i] * distancia; float nx2 = x2[i] * distancia; float ny2 = y2[i] * distancia; line( nx1, ny1, nx2, ny2 ); fractal( nivel-1, nx1, ny1, nx2, ny2 ); }Hecho en Processing
A fines de mostrar el efecto de "fractalización" de los patrones de segmentos, se exponen, a continuación, dos secuencias de fractales con niveles crecientes de iteración:
Figuras: secuencia del proceso recursivo desde 1 hasta 4 estratos
Ejemplo Fractal 03
Figuras: secuencia del proceso recursivo desde 5 hasta 8 estratos
Figuras: secuencia del proceso recursivo desde 9 hasta 11 estratos
Figuras: secuencia del proceso recursivo desde 1 hasta 4 estratos
Figuras: secuencia del proceso recursivo desde 5 hasta 8 estratos
Figuras: secuencia del proceso recursivo desde 9 hasta 11 estratos